I. Ievads
Ūdens var aizdedzināt sveces, vai tā ir taisnība? Tā ir taisnība!
Vai tā ir taisnība, ka čūskas baidās no realgāra? Tas ir nepatiesi!
Šodien mēs apspriedīsim sekojošo:
Vai tā ir taisnība, ka traucējumi var uzlabot mērījumu precizitāti?
Normālos apstākļos traucējumi ir dabisks mērījumu ienaidnieks. Traucējumi samazinās mērījumu precizitāti. Smagos gadījumos mērījumi netiks veikti normāli. No šī viedokļa traucējumi var uzlabot mērījumu precizitāti, kas ir nepareizi!
Tomēr, vai tas vienmēr tā ir? Vai pastāv situācija, kad traucējumi nevis samazina mērījumu precizitāti, bet gan to uzlabo?
Atbilde ir jā!
2. Interferences nolīgums
Apvienojumā ar faktisko situāciju mēs panākam šādu vienošanos par iejaukšanos:
- Traucējumi nesatur līdzstrāvas komponentes. Faktiskajā mērījumā traucējumi galvenokārt ir maiņstrāvas traucējumi, un šis pieņēmums ir pamatots.
- Salīdzinot ar izmērīto līdzstrāvas spriegumu, traucējumu amplitūda ir relatīvi maza. Tas atbilst faktiskajai situācijai.
- Traucējumi ir periodisks signāls jeb vidējā vērtība noteiktā laika periodā ir nulle. Šis apgalvojums ne vienmēr atbilst patiesībai faktiskajos mērījumos. Tomēr, tā kā traucējumi parasti ir augstākas frekvences maiņstrāvas signāls, lielākajai daļai traucējumu ilgākā laika periodā ir pamatoti uzskatīt, ka vidējā vērtība ir nulle.
3. Mērījumu precizitāte traucējumu apstākļos
Lielākā daļa elektrisko mērinstrumentu un skaitītāju tagad izmanto AD pārveidotājus, un to mērījumu precizitāte ir cieši saistīta ar AD pārveidotāja izšķirtspēju. Kopumā AD pārveidotājiem ar augstāku izšķirtspēju ir augstāka mērījumu precizitāte.
Tomēr AD izšķirtspēja vienmēr ir ierobežota. Pieņemot, ka AD izšķirtspēja ir 3 biti un augstākais mērījumu spriegums ir 8 V, AD pārveidotājs ir līdzvērtīgs skalai, kas sadalīta 8 daļās, katra daļa ir 1 V. Šī AD mērījumu rezultāts vienmēr ir vesels skaitlis, un decimālā daļa vienmēr tiek pārnesta vai atmesta, kas šajā rakstā tiek pieņemts kā pārnesta. Pārnešana vai atmešana radīs mērījumu kļūdas. Piemēram, 6,3 V ir lielāks par 6 V un mazāks par 7 V. AD mērījumu rezultāts ir 7 V, un kļūda ir 0,7 V. Mēs šo kļūdu saucam par AD kvantēšanas kļūdu.
Analīzes ērtībai mēs pieņemam, ka skalai (AD pārveidotājam) nav citu mērījumu kļūdu, izņemot AD kvantēšanas kļūdu.
Tagad mēs izmantojam šādas divas identiskas skalas, lai izmērītu divus 1. attēlā parādītos līdzstrāvas spriegumus bez traucējumiem (ideālā situācijā) un ar traucējumiem.
Kā parādīts 1. attēlā, faktiskais izmērītais līdzstrāvas spriegums ir 6,3 V, un kreisajā attēlā redzamajam līdzstrāvas spriegumam nav nekādu traucējumu un tā vērtība ir nemainīga. Labajā attēlā redzamā maiņstrāvas traucētā līdzstrāva, un šajā vērtībā ir zināmas svārstības. Labajā diagrammā redzamais līdzstrāvas spriegums ir vienāds ar kreisajā diagrammā redzamo līdzstrāvas spriegumu pēc traucējumu signāla novēršanas. Sarkanais kvadrāts attēlā apzīmē AD pārveidotāja pārveidošanas rezultātu.

Ideāls līdzstrāvas spriegums bez traucējumiem
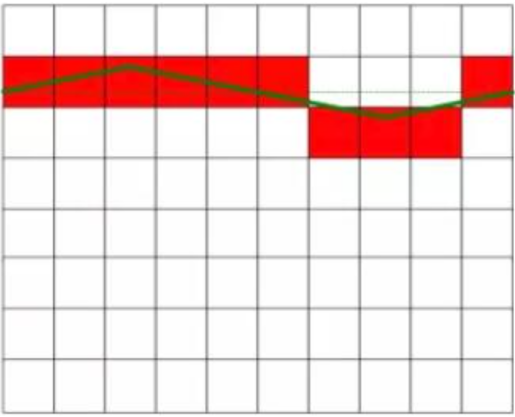
Pielietojiet traucējošu līdzstrāvas spriegumu ar vidējo vērtību nulle
Veiciet 10 līdzstrāvas mērījumus divos iepriekš attēlā redzamajos gadījumos un pēc tam aprēķiniet 10 mērījumu vidējo vērtību.
Pirmā skala kreisajā pusē tiek mērīta 10 reizes, un katru reizi rādījumi ir vienādi. AD kvantēšanas kļūdas ietekmes dēļ katrs rādījums ir 7 V. Pēc 10 mērījumu vidējās vērtības aprēķināšanas rezultāts joprojām ir 7 V. AD kvantēšanas kļūda ir 0,7 V, un mērījumu kļūda ir 0,7 V.
Otrā skala labajā pusē ir dramatiski mainījusies:
Interferences sprieguma un amplitūdas pozitīvā un negatīvā pola atšķirības dēļ AD kvantēšanas kļūda dažādos mērījumu punktos atšķiras. Mainoties AD kvantēšanas kļūdai, AD mērījumu rezultāts mainās no 6 V līdz 7 V. Septiņi no mērījumiem bija 7 V, tikai trīs bija 6 V, un 10 mērījumu vidējais rādītājs bija 6,3 V! Kļūda ir 0 V!
Patiesībā neviena kļūda nav neiespējama, jo objektīvajā pasaulē nav stingra 6,3 V sprieguma! Tomēr tādi patiešām ir:
Ja nav traucējumu, tā kā katrs mērījuma rezultāts ir vienāds, pēc 10 mērījumu vidējās aprēķināšanas kļūda paliek nemainīga!
Kad ir atbilstošs traucējumu daudzums, pēc 10 mērījumu vidējās vērtības aprēķināšanas AD kvantēšanas kļūda samazinās par vienu lieluma kārtu! Izšķirtspēja uzlabojas par vienu lieluma kārtu! Arī mērījumu precizitāte uzlabojas par vienu lieluma kārtu!
Galvenie jautājumi ir šādi:
Vai tas pats ir, ja izmērītais spriegums ir citas vērtības?
Lasītāji varētu vēlēties ievērot otrajā sadaļā sniegto vienošanos par traucējumiem, izteikt traucējumus ar skaitlisku vērtību sēriju, uzlikt traucējumus uz izmērītā sprieguma un pēc tam aprēķināt katra punkta mērījumu rezultātus saskaņā ar AD pārveidotāja pārneses principu, un pēc tam aprēķināt vidējo vērtību verifikācijai, ja vien traucējumu amplitūda var izraisīt nolasījuma izmaiņas pēc AD kvantēšanas, un paraugu ņemšanas frekvence ir pietiekami augsta (traucējumu amplitūdas izmaiņām ir pārejas process, nevis divas pozitīvas un negatīvas vērtības), un ir jāuzlabo precizitāte!
Var pierādīt, ka, ja vien izmērītais spriegums nav tieši vesels skaitlis (tas objektīvajā pasaulē neeksistē), pastāvēs AD kvantēšanas kļūda neatkarīgi no AD kvantēšanas kļūdas lieluma. Ja vien traucējumu amplitūda ir lielāka par AD kvantēšanas kļūdu vai lielāka par AD minimālo izšķirtspēju, mērījuma rezultāts mainīsies starp divām blakus esošām vērtībām. Tā kā traucējumi ir pozitīvi un negatīvi simetriski, samazinājuma un pieauguma lielums un varbūtība ir vienāda. Tāpēc, kad faktiskā vērtība ir tuvāk kurai vērtībai, kuras vērtības parādīšanās varbūtība ir lielāka, un pēc vidējās aprēķināšanas tā būs tuvu kurai vērtībai.
Tas ir: vairāku mērījumu vidējai vērtībai (traucējumu vidējā vērtība ir nulle) jābūt tuvākai mērījumu rezultātam bez traucējumiem, tas ir, izmantojot maiņstrāvas traucējumu signālu ar vidējo vērtību nulle un aprēķinot vairāku mērījumu vidējo vērtību, var samazināt līdzvērtīgās AD kvantēšanas kļūdas, uzlabot AD mērījumu izšķirtspēju un uzlabot mērījumu precizitāti!
Publicēšanas laiks: 2023. gada 13. jūlijs




